11729번: 하노이 탑 이동 순서
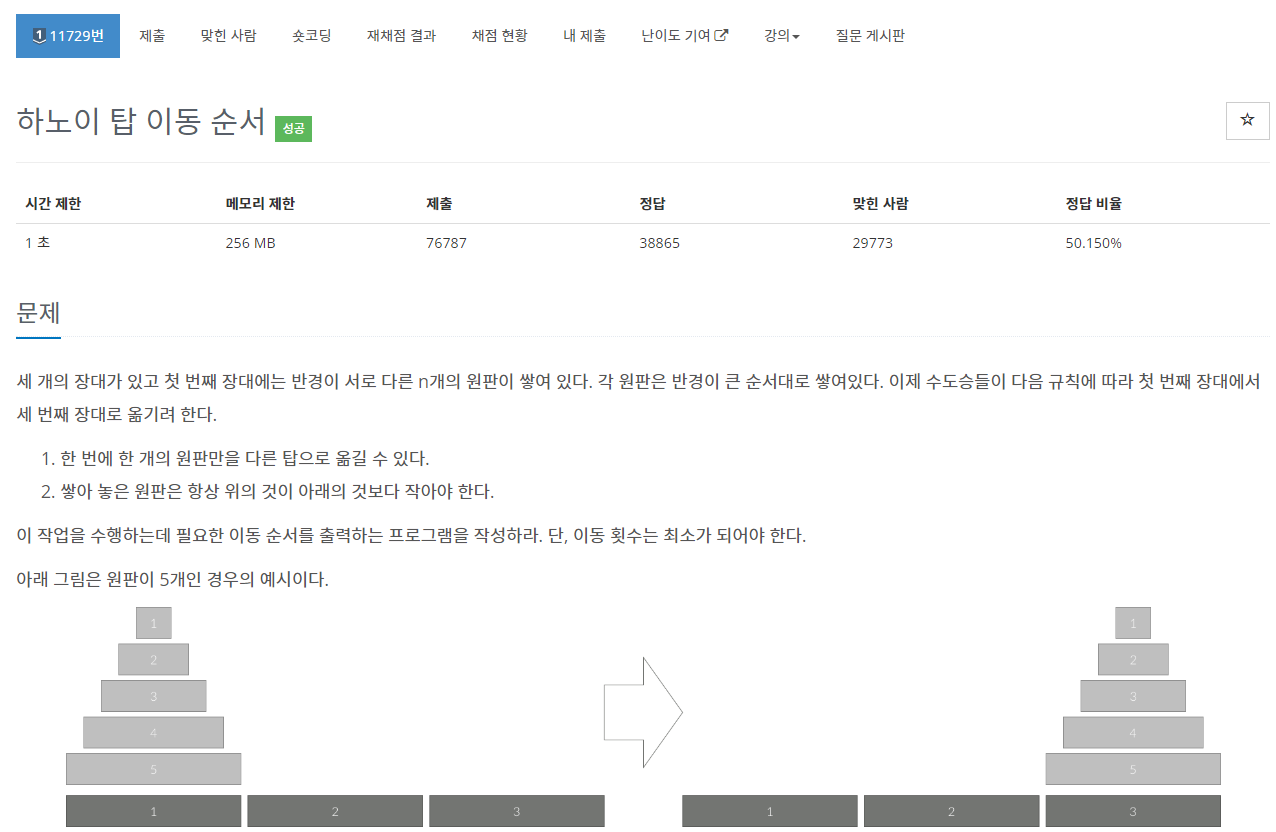
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
한때 킬링타임용으로 하노이탑 어플을 사용하던 때가 있었기에 반가웠던 문제이다. 하노이탑을 옮기는 기본 원리를 알고 있었기에 문제를 이해하는데에 어려움은 없었지만 막상 코드로 구현하려고 하니 처음에는 어려웠다.
하노이탑의 핵심은 규칙을 지키면서 이동을 최소화 하는 것이다. 문제에서 주어진 원판 5개의 경우로 그 방법을 살펴보자.
요구하는 것은 첫 번째 장대에 쌓여 있는 5개의 원판을 세 번째 장대로 옮겨야 한다. 결과적으로 일단 가장 아래에 있는 크기 5의 원판을 세 번째 장대의 가장 아래에 위치시켜야 한다. 그러나 처음 시작할 때에는 크기 5 원판 위에 4개의 원판이 있기 때문에 이 4개의 원판을 두 번째 장대로 먼저 옮겨야 한다.
여기서 한 번 더 생각해보면 현재 크기 5인 원판 위의 4개의 원판을 두 번째 장대로 옮기기 위해서는 먼저 크기 3인 원판이 세 번째 장대에 위치해야 한다. 크기 4인 원판을 옮기기 위해서는 그 위에 어떠한 원판도 존재하면 안되기 때문이다.
크기가 5인 원판을 옮기기 위한 사전 작업으로 크기가 4인 원판을 옮겨야 하고, 크기가 4인 원판을 옮기기 위한 사전 작업으로 크기가 3인 원판을 옮겨야 하고 크기가 3인 원판도 마찬가지로 옮기기 위한 사전 작업으로 그보다 작은 원판들을 옮겨야 한다.
코드로 구현하기 위해 위에서 구술한 일련의 과정을 한 문장으로 정리하자면 크기가 N인 원판을 옮기기 위해서 사전에 크기가 N-1인 원판을 빈 장대로 옮기고, 크기가 N인 원판을 옮긴 후에 한 번 더 크기가 N-1인 원판을 크기가 N인 원판위로 옮기는 과정이 필요하다. 이것을 재귀함수로 구현하는데, 크기가 N인 원판이 옮겨질 때와 크기가 1인 원판이 이동할 때 이동 횟수를 +1 해주고 StringBuilder 객체에 이동한 자취를 저장하고 출력하면 된다.
재귀함수의 종료 조건은 원판의 사이즈가 가장 작을 때로 정하면 된다. 가장 작은 원판 위에는 어떠한 원판도 위치할 수 없기 때문이다.
static void hanoi (int now, int next, int N) {
if (N == 1) {
sb.append(now + " " + next + "\n");
count++;
return;
}
hanoi(now, nextPosition(now+next), N-1);
sb.append(now + " " + next + "\n");
count++;
hanoi(nextPosition(now+next), next, N-1);
}
static int nextPosition (int sum) {
if (sum == 3) return 3;
else if (sum == 4) return 2;
else return 1;
}
처음 문제풀이를 하였을 때에는 위 코드처럼 N-1 크기의 원판이 임시로 위치할 빈 장대를 반환해주는 함수를 별도로 만들어서 해결하였는데 다른 사람의 풀이를 확인해보니 그럴 필요가 없었다. 인수로 전달하는 원판의 현재 위치와 도착 위치를 제외한 빈 장대는 1개뿐이기 때문이다. 불필요하게 코드가 길어지는 것을 지양하는 것은 언제나 어렵게 느껴진다..
전체 코드
import java.util.*;
public class Main {
static StringBuilder sb;
static int count;
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
sb = new StringBuilder();
count = 0;
int N = sc.nextInt();
hanoi(1, 3, 2, N);
System.out.println(count + "\n" + sb);
sc.close();
}
static void hanoi (int now, int next, int mid, int N) {
if (N == 1) {
sb.append(now + " " + next + "\n");
count++;
return;
}
hanoi(now, mid, next, N-1);
sb.append(now + " " + next + "\n");
count++;
hanoi(mid, next, now, N-1);
}
}'백준_JAVA' 카테고리의 다른 글
| [백준] 2156번 - 포도주 시식 (0) | 2023.05.21 |
|---|---|
| [백준] 1932번 - 정수 삼각형 (0) | 2023.05.19 |
| [백준] 2110번 - 공유기 설치 (0) | 2023.05.16 |
| [백준] 1654번 - 랜선 자르기 (0) | 2023.05.16 |
| [백준] 10816번 - 숫자 카드 2 (0) | 2023.05.16 |



