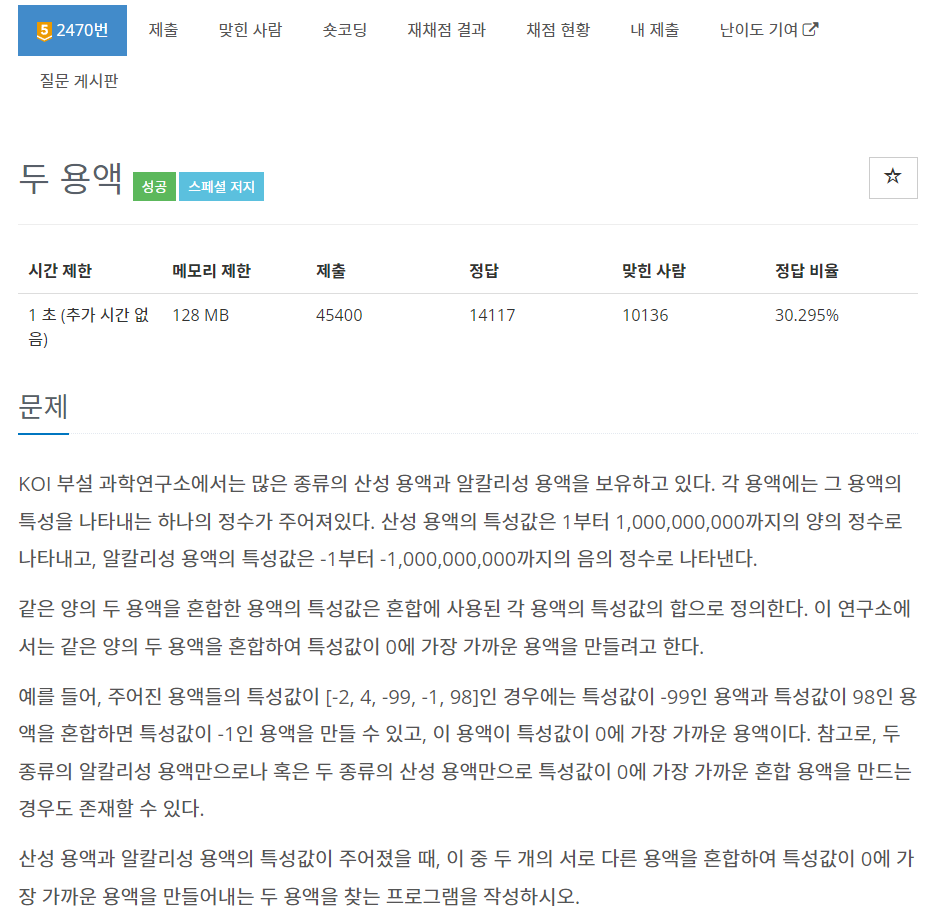
2470번: 두 용액
첫째 줄에는 전체 용액의 수 N이 입력된다. N은 2 이상 100,000 이하이다. 둘째 줄에는 용액의 특성값을 나타내는 N개의 정수가 빈칸을 사이에 두고 주어진다. 이 수들은 모두 -1,000,000,000 이상 1,000,00
www.acmicpc.net
문제
전체 N개의 용액 중 두 용액의 특성값의 합이 0에 가장 가까운 조합을 오름차순으로 출력하시오.
조건
2 <= N <= 100,000
용액의 특성값은 -1,000,000,000 이상 1,000,000,000 이하의 정수
특성값의 합이 0에 가장 가까운 수치를 갖는 조합이 2가지 이상인 경우 아무거나 출력
시간 제한 1초
풀이 방향
완전 탐색으로 풀이할 경우 시간 복잡도 O(N^2)으로 약 100억 번의 연산이 필요하기 때문에 시간 제한에 걸린다. 또한 이미 계산한 조합을 제외하고 부분 완전 탐색을 하더라도 필요한 연산은 약 55억 회이기 때문에 마찬가지로 시간 제한에 발목을 잡힐 것이다. 이 문제의 경우 투포인터를 사용하여 탐색 시간을 O(N)으로 줄이면 해결할 수 있다.
투포인터 사용 이유
문제의 조건을 살펴보자. 두 용액의 특성값의 합이 0에 가장 가까운 조합을 찾아야 하는데, 합이 0에 가장 가깝다는 의미는 다른 말로 두 조합의 합의 절대값의 최소가 답이 될 수 있다는 의미이다. 크게 세 경우로 나누어 생각할 수 있다.
1. 특성값이 음수, 양수가 섞여있는 경우
모든 조합을 살펴보아야 한다.
2. 모든 용액의 특성값이 음수인 경우
이 경우에는 특성값이 가장 큰 용액과 두 번째로 큰 용액의 조합이 답이 된다.
3. 모든 용액의 특성값이 양수인 경우
이 경우에는 특성값이 가장 작은 용액과 두 번째로 작은 용액의 조합이 답이 된다.
사실상 경우 1에 대한 답을 구하는 것이 이 문제의 풀이법일 것이다. 그런데 혹시 특성값이 음수와 양수가 섞여 있으므로 음수와 양수의 조합이 정답이 될 수 있지 않을까? 하는 생각이 든다. 물론 예외가 있긴 하지만 이런 생각을 바탕으로 풀이를 진행해보겠다.
우선 음수와 양수의 합은 서로 상쇄되며 0에 가까워진다. 따라서 우선 특성값 기준 오름차순 정렬을 하여 가장 작은 특성값의 용액과 가장 큰 특성값의 용액의 조합을 확인해본다.

문제에 주어진 예제 입력 1을 오름차순 정렬한 것이다. 여기서 가장 작은 값인 -99과 가장 큰 값인 98의 합의 절댓값은 1이다. 두 합의 결과를 확인했으니 이제 다음 조합을 확인해봐야 하는데 두 가지 방법이 있을 것이다.
i) -99 보다 큰 수와 98의 조합
ii) 98 보다 작은 수와 -99의 조합
두 경우를 모두 확인한다면 완전 탐색과 다를바 없어지기 때문에 하나의 경우에 대해서만 탐색해야 하는데, ii) 보다는 i)을 탐색하는 것이 맞을 것이다. -99와 98 두 수 중에서 절댓값의 크기는 -99가 더 크다. 이 다음의 조합의 합은 현재의 조합 보다 0에 더 가까워지길 기대하기 때문에 0에서 더 멀리 떨어진 -99를 수정하는 것이 나아보인다. 물론 i)에 의한 결과가 현재의 -99와 98 조합의 합보다 0에서 더 멀더라도 문제 없다. 내가 알고 싶은 것은 모든 조합 중에서 0에 가장 가까운 조합이기 때문에 가장 작은 값을 키우고 가장 큰 값을 줄이면서 min을 갱신하면 최종적으로 정답을 구할 수 있다. 이렇게 투포인터를 사용하면 위 세 가지 경우 모두 동등하게 N번만 연산하면 된다.
이전에 해결한 투포인터 문제이다. 위의 문제처럼 용액을 특성값 기준 오름차순 정렬하고 양 끝 요소부터 합이 0에 가장 가까운 조합을 찾아내면 된다.
양 끝 포인터가 가리키는 용액의 특성값의 합이 0에 가장 가까우면 min 값을 갱신하면서 동시에 두 용액의 index를 기록한다. 그러나 만약 그렇지 않다면 양 끝 중 더 절댓값이 더 큰 포인터를 1만큼 반대쪽으로 이동시킨다.
// 용액 특성값의 합은 -2,000,000,000 이상 2,000,000,000 이하이므로 min을 int의 최대값으로 초기화
int min = Integer.MAX_VALUE;
int left = 0;
int right = N-1;
int sol1 = 0;
int sol2 = 0;
while (left < right) {
// 양 끝 포인터가 가리키는 두 용액의 특성값의 합의 절댓값
int value = Math.abs(solution[left] + solution[right]);
// 현재 min보다 작다면 min 갱신
if (value < min) {
min = value;
sol1 = left;
sol2 = right;
// 만약 합이 0이라면 탐색 종료
if (value == 0) break;
}
// 절대값이 큰 포인터를 1만큼 이동시킨다. 또는 포인터 이동 기준을 두 수의 합이 양수인지 음수인지에 따라 판단해도 가능
if (Math.abs(solution[left]) < Math.abs(solution[right]))
right--;
else
left++;
}
위와 같이 오름차순 정렬된 수열의 양 끝을 가리키는 포인터를 설정하고 포인터를 하나씩 이동시키면, 두 용액의 합이 0에 가장 가까운 조합을 찾기 위해 필요한 연산 횟수는 N회이다. 완전 탐색을 사용할 경우 O(N^2)의 시간 복잡도를 갖는 것에 대비하여 시간복잡도가 크게 완화되었다.
그런데 여기서 생각해보아야 할 부분은 용액의 특성값 기준 오름차순 정렬 시 사용한 Arrays.sort 함수이다. 해당 함수의 경우 시간 복잡도가 평균 O(NlogN) 최악 O(N^2) 이기 때문에 최악의 경우에는 정렬하는 과정에서 시간 제한에 걸릴 수 있는 문제가 있는데, 해당 문제의 경우 문제없이 통과한 것을 보면 테스트 케이스에서 정렬에서의 최악의 케이스가 없는 듯 보인다. 만약 Arrays.sort가 안된다면 평균, 최악의 시간 복잡도가 O(NlogN)인 Collections.sort을 이용해야겠다.
전체 코드
import java.util.*;
import java.io.*;
public class Main {
public static void main (String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] solution = new int[N];
String[] input = br.readLine().split(" ");
for (int i = 0; i < N; i++)
solution[i] = Integer.parseInt(input[i]);
Arrays.sort(solution);
int left = 0;
int right = N-1;
int min = Integer.MAX_VALUE;
int sol1 = 0;
int sol2 = 0;
while (left < right) {
int value = Math.abs(solution[left] + solution[right]);
if (value < min) {
min = value;
sol1 = left;
sol2 = right;
if (value == 0) break;
}
if (Math.abs(solution[left]) < Math.abs(solution[right]))
right--;
else
left++;
}
System.out.println(solution[sol1] + " " + solution[sol2]);
br.close();
}
}
'백준_JAVA' 카테고리의 다른 글
| [백준] 11403번 - 경로 찾기 (0) | 2023.06.07 |
|---|---|
| [백준] 1753번 - 최단경로 (1) | 2023.06.06 |
| [백준] 11660번 - 구간 합 구하기 5 (0) | 2023.05.31 |
| [백준] 1018번 - 체스판 다시 칠하기 (0) | 2023.05.31 |
| [백준] 11659번 - 구간 합 구하기 4 (1) | 2023.05.30 |



