1753번: 최단경로
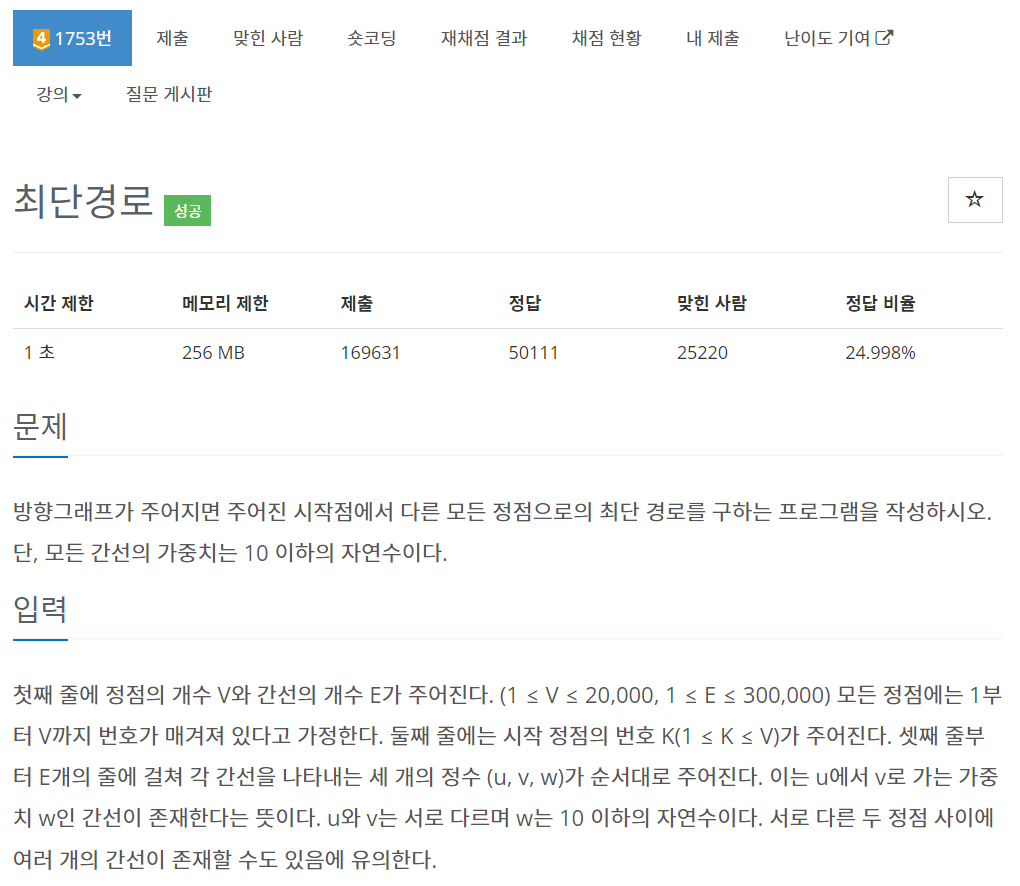
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
다익스트라 알고리즘은 그래프에서 출발 정점으로부터 이동할 수 있는 모든 정점까지의 최단 거리를 구할 때 사용하는 알고리즘 중 한 종류이다. 해당 문제는 다익스트라 알고리즘에 대한 기본 개념을 이해하기에 좋다.
다익스트라 알고리즘에 대한 설명 및 문제 풀이 방법은 아래 글을 참고하자.
[알고리즘] 다익스트라 알고리즘
다익스트라 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로 탐색 알고리즘이다. 간단하게 DFS 혹은 BFS로 구현한 경우 출발 지점에서 도착 지점까지 하나의 경로에 대한 최단 경로
stonage.tistory.com
개인적으로 기록해두고 싶은 점은 그간 그래프나 트리 문제를 풀이할 때에 노드, 간선 등에 대한 정보를 배열의 형태 혹은 Node 클래스를 별도로 생성하는 두 가지 방법을 혼용하였었는데, 별도의 객체를 하나 만들어두고 풀이하는 것이 보다 깔끔한 것 같다.
전체 코드
import java.util.*;
import java.io.*;
public class Main {
static class Node {
int weight, end;
public Node (int weight, int end) {
this.weight = weight;
this.end = end;
}
}
static final int INF = Integer.MAX_VALUE;
public static void main (String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] input = {};
input = br.readLine().split(" ");
int V = Integer.parseInt(input[0]);
int E = Integer.parseInt(input[1]);
int K = Integer.parseInt(br.readLine());
List<Node>[] link = new ArrayList[V+1];
for (int i = 1; i <= V; i++) link[i] = new ArrayList<>();
for (int i = 0; i < E; i++) {
input = br.readLine().split(" ");
int u = Integer.parseInt(input[0]);
int v = Integer.parseInt(input[1]);
int w = Integer.parseInt(input[2]);
link[u].add(new Node(w, v));
}
int[] dp = new int[V+1];
Arrays.fill(dp, INF);
PriorityQueue<Node> que = new PriorityQueue<>((a, b) -> {
return a.weight - b.weight;
});
que.offer(new Node(0, K));
while (!que.isEmpty()) {
Node u = que.poll();
for (Node v : link[u.end]) {
int sum = u.weight + v.weight;
if (dp[v.end] > sum) {
dp[v.end] = sum;
que.offer(new Node(sum, v.end));
}
}
}
StringBuilder sb = new StringBuilder();
for (int i = 1; i <= V; i++) {
if (i == K)
sb.append(0 + "\n");
else if (dp[i] == INF)
sb.append("INF" + "\n");
else
sb.append(dp[i] + "\n");
}
System.out.println(sb);
br.close();
}
}'백준_JAVA' 카테고리의 다른 글
| [백준] 11404번 - 플로이드 (1) | 2023.06.07 |
|---|---|
| [백준] 11403번 - 경로 찾기 (0) | 2023.06.07 |
| [백준] 2470번 - 두 용액 (0) | 2023.06.05 |
| [백준] 11660번 - 구간 합 구하기 5 (0) | 2023.05.31 |
| [백준] 1018번 - 체스판 다시 칠하기 (0) | 2023.05.31 |



