다익스트라 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로 탐색 알고리즘이다. 간단하게 DFS 혹은 BFS로 구현한 경우 출발 지점에서 도착 지점까지 하나의 경로에 대한 최단 경로를 확인할 수 있던 것에서 확장하여 출발 지점에서 이동할 수 있는 모든 지점에 대한 최단 경로를 알아낼 수 있다.
다익스트라 알고리즘을 적용할 수 있는 자료구조는 그래프이고 동작 단계는 다음과 같다.
1. 그래프 상의 모든 정점과 간선, 가중치에 대한 정보를 저장한다.
2. 최단 거리 테이블(dp)을 초기화 한다. 이때 dp에는 허용할 수 있는 가장 큰 수 + 1가 저장되어 있다.
3. 출발 노드에 대한 정보를 A에 저장한다(보통은 A = 우선순위 큐).
4. A에서 누적 가중치가 가장 작은 경로에서 (초기에는 출발노드) 방문할 수 있는 정점(초기에는 출발 노드와 인접한 정점)의 최단 거리 테이블을 갱신할 수 있다면 갱신한다.
5. 4 과정을 더 이상 탐색할 간선이 없을 때까지 반복한다.
// V = 정점의 갯수, 정점은 1 ~ V 의 번호를 갖는다.
int[] dp = new int[V+1];
// 최단 경로 테이블 초기화.
Arrays.fill(dp, INF);
// 다음에 이동할 수 있는 정점에 대한 정보를 누적 가중치 기준 오름차순 정렬하여 저장하는 객체
PriorityQueue<Node> que = new PriorityQueue<>((a, b) -> {
return a.weight - b.weight;
});
// K = 출발 정점
que.offer(new Node(0, K));
// dp를 갱신할 수 있다면 반복
while (!que.isEmpty()) {
// 현재 누적 가중치가 가장 작은 정점
Node u = que.poll();
for (Node v : link[u.end]) {
int sum = u.weight + v.weight;
// 만약 최단 경로 테이블(dp)을 갱신할 수 있다면 갱신 후 큐에 해당 경로에 대한 정보를 담는다.
if (dp[v.end] > sum) {
dp[v.end] = sum;
que.offer(new Node(sum, v.end));
}
}
}
내가 생각하는 다익스트라 알고리즘의 가장 기본 형태이다. 이를 토대로 필요에 따라 방문처리를 추가하여 사용하기도 한다.
다음은 위의 코드가 실질적으로 어떻게 동작하는지 그림과 함께 간단하게 살펴보겠다. 다음과 같은 방향 그래프가 존재하고 출발 노드가 1인 경우 출발 정점으로부터 그 외 모든 정점까지의 최단 경로를 구해본다.
해당 그래프는 백준 1753번 최단경로 문제의 예제이다.
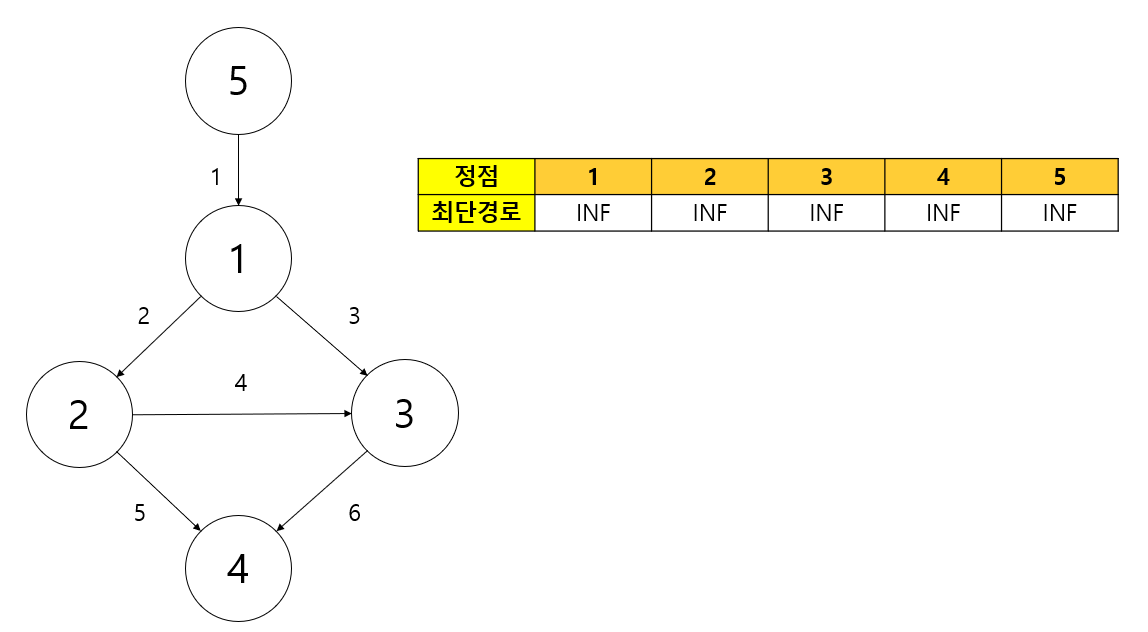
테이블은 최단 경로 테이블(dp)을 의미하고 왼쪽은 방향 그래프의 연결 상태와 가중치에 대한 정보이다. 최단 경로 테이블의 INF는 허용할 수 있는 가장 큰 데이터 + 1를 의미한다.
우선 출발노드부터 탐색을 시작한다.
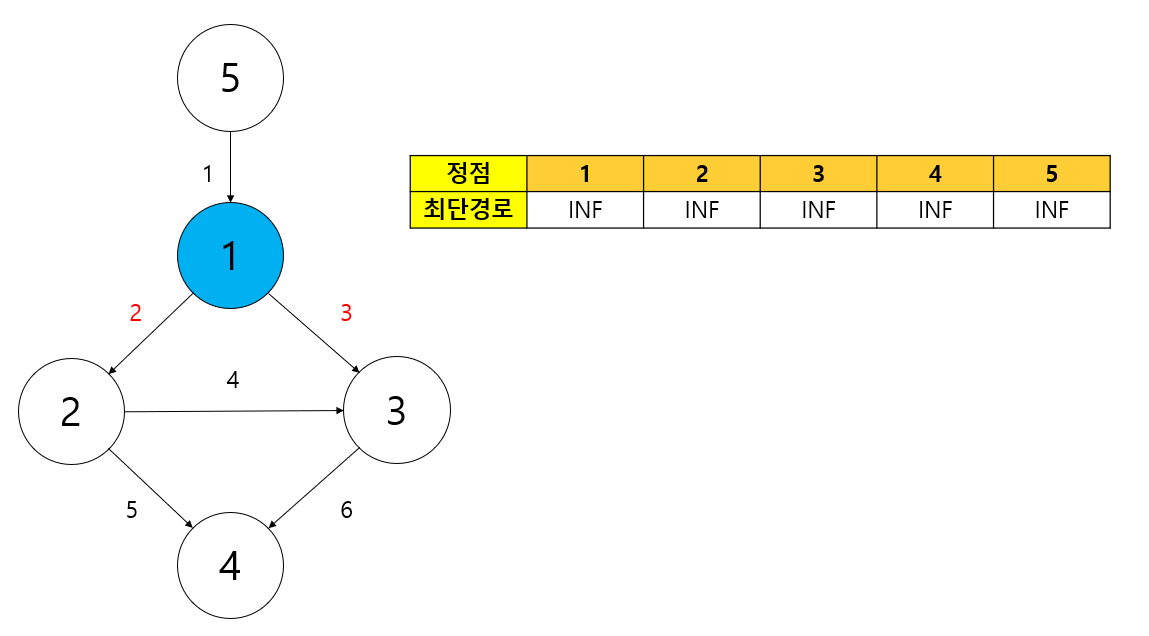
현재 1번 노드에서 이동할 수 있는 정점은 2번, 3번이다.
2번 정점에 대하여 먼저 고려해보면, 1 -> 2 경로의 누적 가중치는 2이고 이는 현재 최단 경로 테이블의 dp[2] 값보다 작다. 따라서 dp[2] = 2 으로 갱신하고 큐에 2번 정점까지의 경로에 대한 정보를 담는다.
1 -> 3 경로도 마찬가지로 현재 최단 경로 테이블의 dp[3] 값보다 작으므로 dp[3] = 3 으로 갱신하고 큐에 3번 정점까지의 경로에 대한 정보를 담는다.
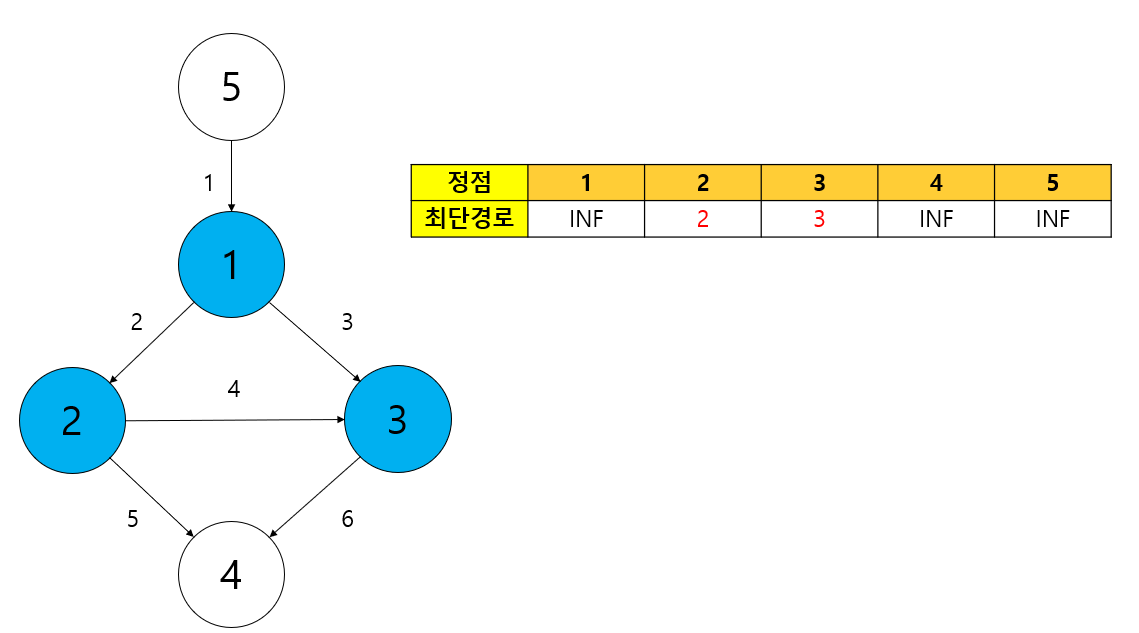
현재 큐에는 2번, 3번 정점까지의 경로에 대한 최단거리 정보가 들어있다. 다음번 반복에는 우선순위 큐의 특성상 누적 가중치가 더 작은 정점에 대한 정보가 poll되기 때문에 2번 정점에 대한 탐색을 이어나간다.

2번 정점에서 이동할 수 있는 경로는 2 -> 3 과 2 -> 4 이다.
2 -> 3 경우에는 2번 정점까지의 최단 경로 2에 2 -> 3 경로 가중치의 합 4의 합인 6이 3번 정점까지의 최단 경로 dp[3] 보다 크다. 따라서 이 경우에는 갱신하지 않는다.
2 -> 4 경우에는 4번 정점까지의 누적 가중치 합인 7이 dp[4] 의 값보다 작기 때문에 갱신이 가능하다. 따라서 dp 테이블을 갱신 후 큐에 4번 정점까지에 대한 정보를 담는다.

4번 정점에서 이동할 수 있는 경로는 존재하지 않는다. 따라서 탐색이 종료된다.
1번 정점은 출발 정점이기 때문에 최단 경로는 0이 되고 5번 정점의 경우 최단 거리 테이블이 갱신된 적이 없기 때문에 출발 정점에서 도달할 수 없는 정점이 된다.
이런 다익스트라 알고리즘은 흔히 인공위성 GPS 소프트웨어 등에서 사용된다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 최소 공통 초상(LCA) (0) | 2023.06.11 |
|---|---|
| [알고리즘] 위상 정렬 (0) | 2023.05.24 |
| [알고리즘] 유니온 파인드(Union Find) (0) | 2023.05.24 |
| [알고리즘]최소 신장 트리(Minimum Spanning Tree) (1) | 2023.05.22 |



