Lowest Common Ancestor
한국말로 직역하면 최소 공통 조상이다. 자료구조 트리에 사용하며, 트리 내 두 노드 u, v의 공통 부모 중 가장 가까운 노드를 찾고자 할 때 사용할 수 있는 알고리즘의 한 유형이다.
간단한 그림으로 LCA의 한 예시를 보여주겠다.
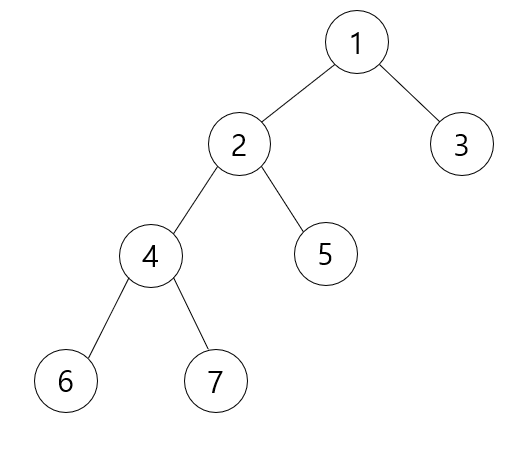
1번 노드를 루트노드로 하는 위와 같은 트리가 있을 때, 6번 노드와 5번 노드의 최소 공통 조상인 LCA(5, 6)은 2번 노드이다.

LCA의 정의에 대해서 간단히 살펴봤으므로 다음은 LCA가 어떻게 동작하는지 알아보겠다.
일반적으로 트리 관련 문제에서는 두 정점을 잇는 간선에 대한 정보가 주어진다. 그리고 간선에 대한 정보를 사용하여 이중 배열 또는 리스트 타입 배열 객체를 사용하여 전체 트리 구조를 저장할 수 있다. 만약 처음부터 두 정점간에 부모 - 자식 관계를 알 수 있다면 LCA를 수행함에 있어 한결 수월해 지겠지만 단순히 연결 정보만 주어지더라도 상관은 없다. 루트 노드를 찾은 다음 앞서 저장한 트리 정보를 바탕으로 부모 - 자식 관계의 노드를 parent[] 배열에 저장하면 되기 때문이다.
모든 정점에 대한 부모 - 자식 관계에 대한 정보를 parent 배열에 저장하였다면 본격적으로 LCA를 수행하면 되는데, 원리는 다음과 같다.
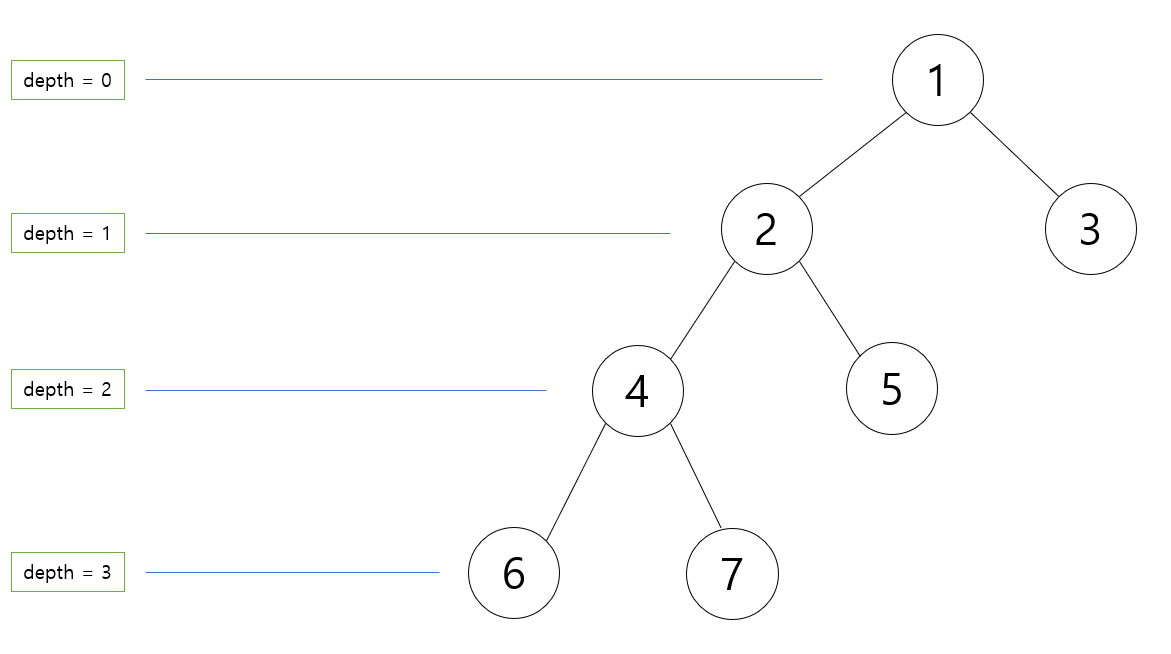
우선 루트 노드의 깊이 0 기준 구하고자 하는 두 노드의 깊이를 알아내야 한다. 트리에는 루트 노드로 부터 얼마나 떨어져 있는지를 나타내는 깊이라는 개념이 존재하는데, 특정 노드에 대한 깊이는 앞서 생성한 parent[] 배열을 따라 루트 노트까지 도달하면 알 수 있다.
private int calDepth (int node) {
int depth = 0;
// 루트노드가 1번이고, parent[1] = 0 인 상태이다.
while (parent[node] != 0) {
node = parent[node];
depth++;
}
return depth;
}
두 노드의 깊이를 알아냈다면 우선 두 노드의 깊이를 같게 만들어야 한다. 앞서 보았던 그림과 함께 그 이유를 말해보자면
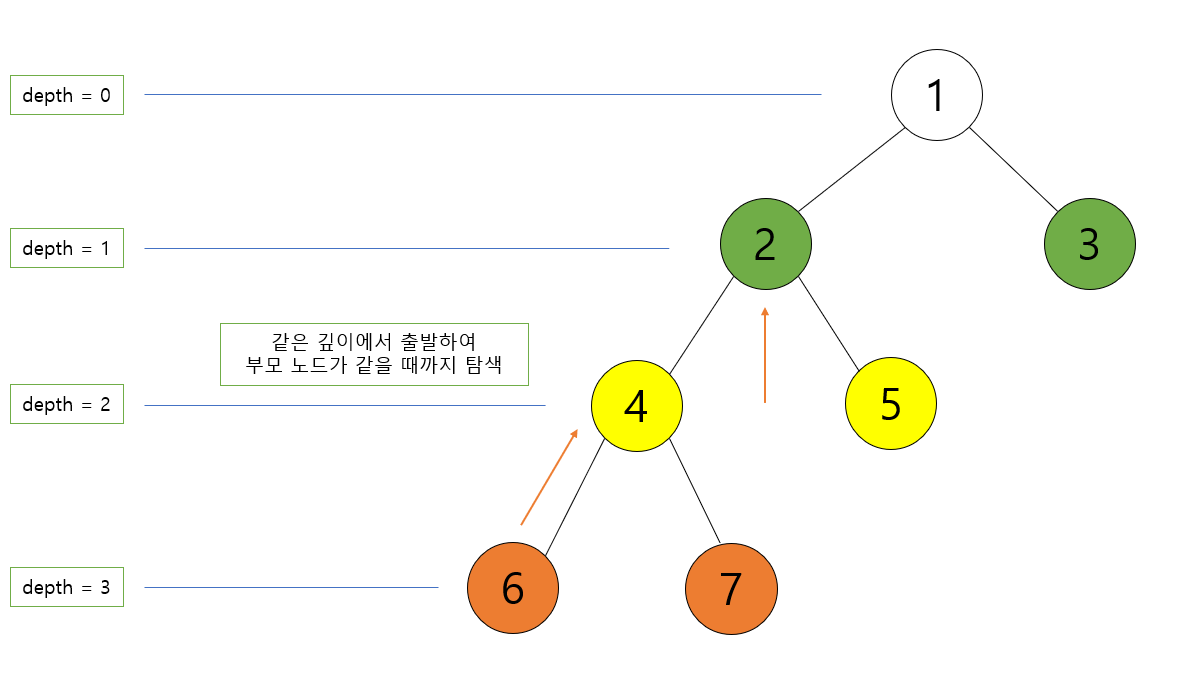
LCA(5, 6) 에서 6번 노드는 현재 깊이가 3이고 5번 노드는 깊이가 2이다. 만약 두 노드의 깊이가 같다면 부모가 같을 때까지 각각 깊이를 1개씩 줄이면 되겠지만 현상태에서는 두 노드의 깊이가 다르기 때문에 불가능하다. 따라서 두 노드의 깊이를 맞춰주기 위해 6번 노드의 깊이를 5번 노드의 깊이와 동일한 2로 만들어 주어야 한다.
parent[6] = 4이고 이제 두 노드의 깊이가 같아졌으므로 두 노드의 첫 공통 부모가 나올 때까지 깊이를 하나씩 줄여주면 된다.
코드로 구현하면 아래와 같다.
// 위 예시에서 5, 6번 노드가 인수로 전달된다.
private int LCA (int u, int v) {
int u_depth = calDepth(u);
int v_depth = calDepth(v);
// 두 노드 중 깊이가 더 깊은 노드를 첫 번째 인자, 얕은 깊이 노드를 두 번째, 두 노드간의 깊이 차이를 세 번째 인자로 전달
if (u_depth > v_depth)
return findCommonParent(u, v, u_depth-v_depth);
else
return findCommonParent(v, u, v_depth-u_depth);
}
private int findCommonParent (int u, int v, int interval) {
// 두 깊이의 차이가 0이 될때까지 깊이가 더 깊은 u 노드의 깊이를 줄인다.
while (interval-- > 0)
u = parent[u];
// 두 노드의 첫 공통 부모를 찾을 때까지 탐색하여 반환
while (u != v) {
u = parent[u];
v = parent[v];
}
return u;
}
위와 같은 과정을 거치면 트리에서 임의의 두 정점의 최소 공통 조상을 구할 수 있게 된다.
이번에 살펴본 예시는 단 하나의 쌍에 대한 LCA를 구했지만, 정점의 수가 많아지고 하나의 트리에서 구해야 하는 정점의 쌍이 많다면 다이나믹 프로그래밍, 이분 탐색 등을 활용하면 반복적인 연산에서 보다 효율적으로 LCA를 구할 수 있을 것이다.
아래 문제들을 풀어보면서 LCA에 대한 학습을 해볼 수 있다.
1. 효율성은 신경쓰지 않고 하나의 정점 쌍에 대한 LCA를 구현해볼 수 있는 문제
3584번: 가장 가까운 공통 조상
루트가 있는 트리(rooted tree)가 주어지고, 그 트리 상의 두 정점이 주어질 때 그들의 가장 가까운 공통 조상(Nearest Common Anscestor)은 다음과 같이 정의됩니다. 두 노드의 가장 가까운 공통 조상은, 두
www.acmicpc.net
2. 최대 10,000개의 정점 쌍에 대한 LCA를 찾아야 하는 문제. 1번보다 효율적인 방법이 필요하다.
11437번: LCA
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
3. 정점의 수가 최대 100,000개, 두 노드의 쌍이 최대 100,000개인 LCA 문제. 2번 문제보다 더 효율적인 방법이 필요하다.
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
'알고리즘' 카테고리의 다른 글
| [알고리즘] 다익스트라 알고리즘 (0) | 2023.06.06 |
|---|---|
| [알고리즘] 위상 정렬 (0) | 2023.05.24 |
| [알고리즘] 유니온 파인드(Union Find) (0) | 2023.05.24 |
| [알고리즘]최소 신장 트리(Minimum Spanning Tree) (1) | 2023.05.22 |



