연결그래프
모든 정점이 연결되어 있는 그래프를 연결 그래프라고 부른다. 여기서 '연결되어 있다'라는 것의 의미는 인접한 정점만을 의미하는 것이 아니라 다른 정점을 거쳐서 도달 할 수 있음을 포함한다.
반대로 어느 두 정점을 골랐을 때 상호간에 도달할 수 없는 경우가 존재하는 그래프를 비연결 그래프라고 한다.


Spanning Tree
무방향 연결 그래프 내의 모든 정점을 연결하고 사이클이 없는 그래프를 의미하며 신장 트리라고도 부른다. N개의 정점을 가지는 그래프의 최소 간선의 수는 N-1 개이고, 신장 트리의 간선 수는 언제나 N-1개가 된다.
신장 트리를 찾는 방법은 DFS, BFS 등이 있고 하나의 그래프에는 복수개의 신장 트리가 존재할 수 있다.
이런 신장 트리를 적용할 수 있는 분야는 사내 통신 네트워크 구축시 가장 적은 수의 케이블을 사용하여 모든 통신라인을 연결하고자 하는 경우 사용한다.
Minimum Spanning Tree
신장 트리의 확장 개념으로 그래프 내 각 간선의 가중치 합이 최소가 되는 신장트리이며 최소 신장 트리라고 부른다. 최소 신장 트리의 대표적인 알고리즘은 프림 알고리즘과 크루스칼 알고리즘이 있다. 두 알고리즘의 응용면에 있어 상황에 따라 효율성이 달라질 수 있기 때문에 둘 다 알아두는 것이 좋다.
Kruskal's algorighm
크루스칼 알고리즘은 순간마다 최선의 선택을 지향하는 그리디 알고리즘에 속하며 주어진 무방향 그래프의 최소 신장 트리를 구할 때 사용한다. 우선 가중치 기준 오름차순으로 정렬하고난 뒤, 사이클을 형성하지 않는다면 정렬된 순서대로(가중치가 작은) 간선을 선택한다.
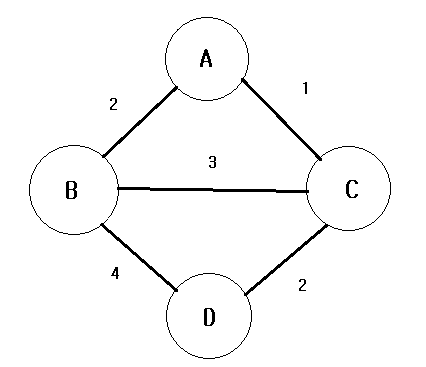
위와 같은 그래프가 존재할 때의 경우를 살펴보자. 간선의 가중치 기준 오름차순으로 정렬한다면 다음과 같다.
| A-C | A-B | C-D | B-C | B-D |
| 1 | 2 | 2 | 3 | 4 |
그 다음 가중치가 가장 작은 A-C 간선을 선택한다.
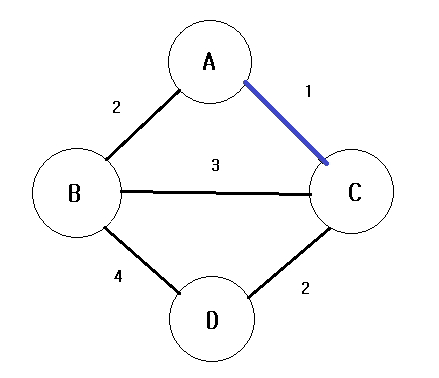
그 다음 작은 가중치를 갖는 A-B와 C-D 을 선택한다.
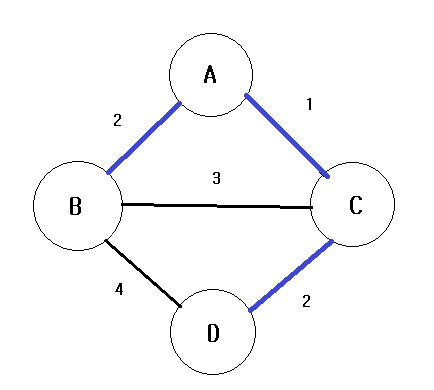
예시로 든 그래프가 운이 좋게 가중치가 가장 낮은 것부터 3개의 간선을 선택했을 때 최소 신장트리를 형성하였다. 그 다음 낮은 가중치를 갖는 간선을 선택하게 되면 어떻게 되는지도 살펴보자.
그 다음 작은 가중치를 갖는 간선은 B-C 인데, B-C를 연결하게 되면 이 그래프는 사이클을 갖게 된다.
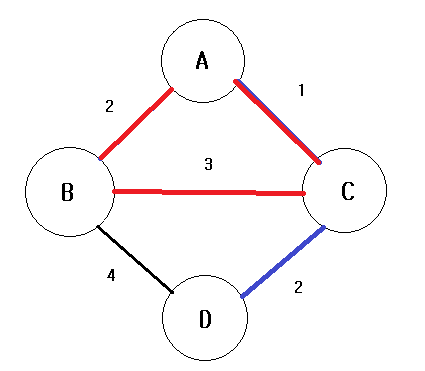
신장 트리는 그래프가 사이클을 형성하면 안되므로 B-C 간선을 잇는 최소 신장 트리는 존재하지 않게 된다.
Prim's algorithm
프림 알고리즘 그리디 알고리즘에 속하며, 최소 신장 트리를 찾는 하나의 방법이다. 프림 알고리즘은 주어진 그래프 내의 정점을 트리집합에 속한 정점들과 인접한 정접의 두 집합 그룹으로 나누어 진행한다.
트리 집합에 속한 정점들의 그룹을 T라고 할 때, 우선 아무 정점을 골라서 T에 넣는다. 그 다음 트리 집합에 속한 정점들과 트리 집합을 구성하는 정점들과 연결된 간선이 존재하는 인접 정점들 중 가장 낮은 가중치의 간선과 연결된 정점에 대해 간선과 정점을 T 집합에 넣는다.
위 과정을 처음 주어진 그래프의 모든 정점들이 T에 들어갈 때까지 반복하면 최소 신장 트리를 구할 수 있다.
크루스칼 알고리즘을 설명할 때 사용한 그래프를 재사용하여 프림 알고리즘의 예시를 들겠다. 시작 정점이 A라고 할 때, A 정점을 집합 T에 넣는다. 이때 집합 T에는 정점 A만이 존재한다. 두 그룹을 시각적으로 구분하기 위해 집합 T에 속한 정점을 노란색으로, 아직 T에 속하지 않은 정점을 흰색으로 구분하겠다.
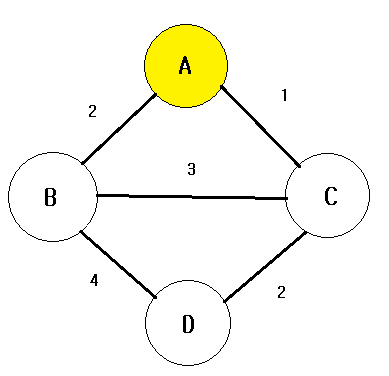
그 다음 집합 T에 속해 있는 정점과 인접한 정점들의 간선 가중치를 비교한다. A와 인접한 정점은 B와 C이고 그 중에서 가중치가 최소인 간선은 A 와 C를 잇는 간선이다. 따라서 정점 C를 집합 T에 넣는다.

현재 집합 T에는 A, C 두 정점이 속해있다. 이 두 정점과 인접한 정점간의 간선은 A-B, B-C, C-D가 있고 이 중 가중치가 가장 작은 간선은 A-B와 C-D 이다. 최소 신장트리의 모양은 1개 이상일 수 있고 두 간선 중 어느 것을 택해도 최종적인 가중치의 합에는 영향을 주지 않는다.
A-B를 택한 경우로 진행하겠다. 정점 B를 집합 T에 넣는다.
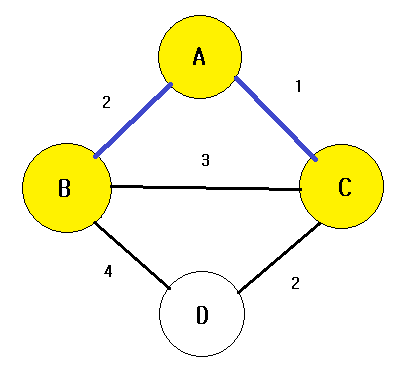
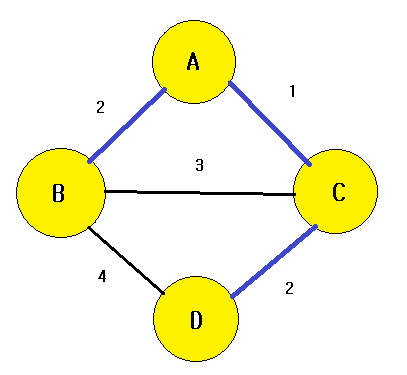
마지막으로 아직 집합 T에 속하지 않은 정점 D에 대해서 가중치가 가장 작은 C-D를 연결하면 처음 주어진 그래프의 모든 정점이 집합 T에 속하게 되고, 최소 신장 트리를 구하게 된다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 최소 공통 초상(LCA) (0) | 2023.06.11 |
|---|---|
| [알고리즘] 다익스트라 알고리즘 (0) | 2023.06.06 |
| [알고리즘] 위상 정렬 (0) | 2023.05.24 |
| [알고리즘] 유니온 파인드(Union Find) (0) | 2023.05.24 |



